Research overview of formation and heat transfer of slag film in mold during continuous casting
-
摘要:
介绍了模拟结晶器内渣膜形成的实验方法, 综述了国内外学者在保护渣传热方面所做的研究工作, 包括固态渣膜的界面热阻、保护渣的导热系数、辐射传热以及渣膜的光学性质, 并提出了今后在渣膜形成及传热研究中有待进一步完善的内容和方向.现有的研究结果表明利用热丝法可以对渣膜的形成过程进行原位观察, 采用水冷铜探头法可以获取用于研究渣膜微观组织的固态渣膜样品.渣膜的界面热阻在0.0002~0.002 m2·K·W-1之间.在800℃以下, 保护渣的导热系数在1.0~2.0 W·m-1·K-1范围内, 且随温度的升高而逐渐增加.渣膜中的晶体一方面可以增加渣膜的界面热阻, 另一方面可以提高固态渣膜的反射率, 起到降低辐射热流的作用.此外, 过渡族金属氧化物的加入以及固态渣膜中弥散分布的微小颗粒也能改变渣膜的光学性质, 从而影响通过渣膜的辐射传热.
Abstract:Mold flux, which plays an important role in continuous casting, occurs when liquid slag on top of the molten steel infiltrates the gap between the shell and mold. During this process, a liquid slag film forms on the shell side, whereas a solid slag film forms on the mold side. The behavior of the slag film between the shell and mold has a significant effect on the sequence casting and quality of the slab surface. To investigate the in-mold behavior and heat transfer of slag film, researchers have simulated the formation of slag film in the laboratory. Measurements and theoretical calculations have been performed to study the heat transfer of slag film. In this paper, the experimental methods used to simulate the formation of slag film were described and the research related to heat transfer in slag film was summarized, including the interfacial thermal resistance, the thermal conductivity of the mold flux, radiative heat transfer, and optical properties of the slag film. The issues related to the formation and heat transfer of slag film were also identified, that require further investigation. The results of recent studies indicate that the hot thermocouple technique could be applied to observe the formation of slag film, and the copper-finger dig test could be used to obtain samples for investigations related to the microstructure of solid slag film. The interfacial heat resistance is reported to be between 0.0002 and 0.002 m2·K·W-1. The thermal conductivity of mold flux at 800℃ ranges from 1.0-2.0 m2·K·W-1, and increases with increased temperature. Crystals in the solid slag film not only increase the interfacial heat resistance, but also decrease the radiative heat flux by reducing the reflectivity of slag film. Furthermore, due to the resulting change in optical properties, the addition of transition metal oxides and fine particles dispersed in slag film may also influence the radiative heat transfer through slag film.
-
Keywords:
- continuous casting /
- mold flux /
- slag film /
- interfacial thermal resistance /
- radiation
-
结晶器保护渣是连铸过程中使用的一种重要功能材料，主要由基料(CaO和SiO2)，助熔剂(苏打和萤石)和炭质材料(炭黑和石墨)构成，在浇铸过程中主要有以下五个冶金功能：(1) 绝热保温防止钢液面结壳；(2) 防止钢液二次氧化；(3) 吸收上浮夹杂；(4) 润滑铸坯；(5) 控制坯壳与结晶器之间的水平传热[1-2]. 其中，润滑铸坯主要依靠铸坯一侧的液态渣膜实现，而控制传热主要依靠结晶器一侧的固态渣膜实现[3]. 液渣膜过薄或液渣黏度过大可能会引起黏结漏钢，而固态渣膜控热能力不足可能会导致铸坯表面出现凹陷或裂纹等表面质量问题[4]. 可见，坯壳与结晶器之间渣膜的行为不仅关系到浇铸能否顺行，对铸坯的表面质量也有重要影响. 为了研究结晶器内渣膜的行为及传热机理，国内外学者在实验室模拟了渣膜的形成，并对渣膜传热进行了测试及理论计算. 本文介绍了模拟结晶器内渣膜形成的几种实验方法，并综述了国内外学者在保护渣传热方面所做的研究工作，包括界面热阻、导热系数、以及辐射传热的测试及计算方法.
1. 结晶器内渣膜形成过程的模拟
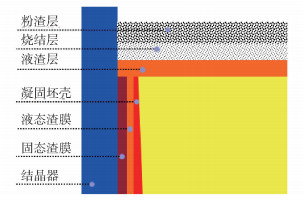
保护渣在结晶器内的状态和分布如图 1所示. 在工业现场很难观察到结晶器内渣膜的行为，但可以通过数值计算和实验方法模拟结晶器内渣膜的形成过程. Thomas数值计算的结果表明[5]，弯月面处铸坯表面液渣的温度高于1400 ℃，而结晶器壁的温度较低，一般不超过300 ℃. 在温度较高的铸坯一侧，液渣随坯壳一同向下运动，而远离坯壳一侧的液渣由于黏度较大，随结晶器上下往复振动. 液渣完全凝固之后将在靠近结晶器一侧形成1~2 mm厚的固态渣膜. 靠近结晶器一侧的固渣膜表面的温度在400~800 ℃之间，且越往下渣膜表面温度越低. 结晶器上部的固态渣膜较薄，随结晶器一同上下往复振动，距弯月面250 mm以下的固态渣膜与结晶器之间存在相对运动，但相对运动速度小于1 mm·s-1.
模拟渣膜形成的实验方法主要有两种，一种是模拟坯壳与结晶器之间的温度分布，从而对渣膜的形成过程进行原位观察；另一种是通过模拟结晶器的冷却条件获取能用于分析固态渣膜组织结构的渣膜样品. 前者主要通过双丝法(double hot thermocouple technique)实现，而后者可以利用水冷铜探头法实现.
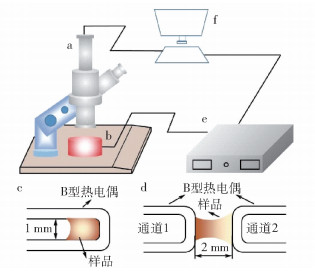
Kashiwaya等最早将热丝法用于保护渣的研究，利用热电偶既可以对保护渣进行加热又可以测温的特点在两根热电偶之间的液渣内建立一个温度梯度，通过摄像机拍摄的照片可以对渣膜的形成过程进行原位观察[6]. 实验装置如图 2所示.
![]()
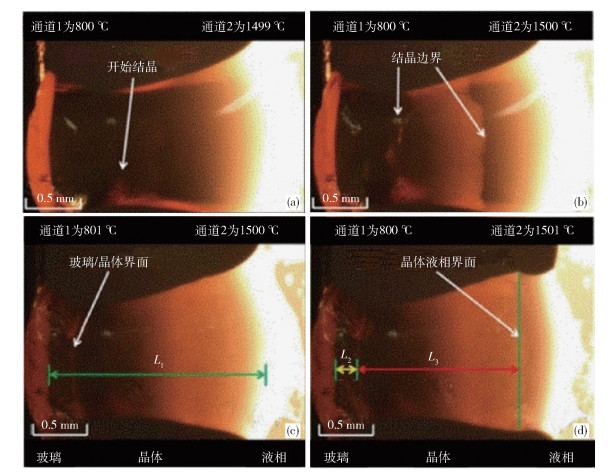
图 2 热丝法实验装置示意图. (a) 工业摄像机；(b) 样品室；(c) 单热电偶；(d) 双热电偶；(e) 加热装置；(f) 计算机Figure 2. Schematic diagram of experimental apparatus for hot thermocouple technique: (a) industrial camera; (b) sample chamber; (c) single hot thermocouple; (d) double hot thermocouple; (e) hot thermocouple driver; (f) computer双丝法测试过程中两根热电偶之间的距离控制在2 mm左右，其中一根热电偶在加热到1500 ℃后温度保持不变，模拟坯壳一侧液渣的温度条件，而另一根热电偶加热到1500 ℃后保温一段时间，然后快速冷却到800 ℃，模拟结晶器一侧固态渣膜的温度条件[7]. 当两根热电偶的温度到达设定温度以后，晶体开始在低温一侧析出，然后向高温一侧迁移. 当热电偶恒温一段时间以后，可以观察到靠近高温热电偶一侧形成的液渣层，位于两根热电偶中间的结晶层以及靠近低温热电偶一侧形成的玻璃层[8-9]，如图 3所示.
![]()
图 3 双丝法模拟的渣膜形成过程, 其中通道1和2分别为模拟结晶器侧固渣温度和坯壳侧液渣温度条件. (a) 10 s；(b) 50 s；(c) 300 s；(d) 301 s[10]Figure 3. Formation process of slag film simulated by DHTT, where Channel 1 and 2 simulate the temperature condition of solidified slag film near the mold wall and liquid slag near the shell, respectively: (a) 10 s; (b) 50 s; (c) 300 s; (d) 301 s[10]图 3中L1为渣膜总长度(m)，L2为玻璃层的长度(m)，L3为结晶层的长度(m). 可以将结晶层与玻璃层之和与渣膜总长度的比值定义为凝固分数：
$$ F_{\mathrm{s}}=\frac{L_{2}+L_{3}}{L_{1}} $$ (1) 式中，Fs表示凝固分数. 而结晶层长度与固渣层长度(结晶层与玻璃层长度之和)的比值可以定义为结晶分数：
$$ F_{\mathrm{c}}=\frac{L_{3}}{L_{2}+L_{3}} $$ (2) 式中，Fc表示结晶分数. 渣膜的凝固分数可用于反映渣膜对坯壳的润滑效果，凝固分数越大，液渣层的厚度越薄，润滑效果也就越差[10].
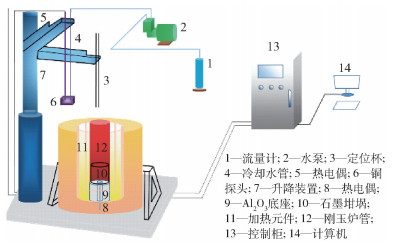
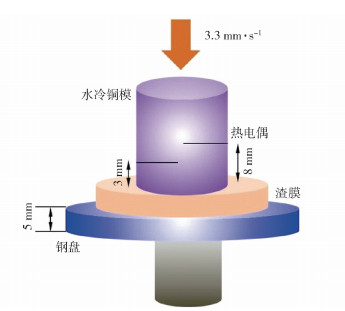
为了研究渣膜形成过程中的传热行为，Wen等利用浸入式水冷铜探头对液渣进行冷却[11-12]，通过进出水温差计算热流密度. 实验设备如图 4所示. 这种方法获得的固态渣膜的微观组织结构与工业现场获得的渣膜的微观组织结构是相似的. 在扫描电镜下可以观察到渣膜不同位置处晶体尺寸及分布情况是不相同的. 靠近铜探头一侧晶体密集，且尺寸较小，而靠近液渣一侧的晶体以树枝状和块状为主，如图 5所示. 与双丝法相比，水冷铜探头法更偏向于液渣凝固过程的模拟，测试过程中不能观察到渣膜的形成过程，但测得的热流密度可以作为传热计算的边界条件，将数值计算得到的温度分布与结晶动力学相结合可以推测出固态渣膜的形成过程. 计算结果表明[13]，液渣凝固过程中的冷却速度是随时间变化的. 凝固初期，液渣冷却速度随时间逐渐增加，最大值超过50 ℃·s-1. 凝固后期液渣冷却速度小于1 ℃·s-1. 结合单丝法(single hot thermocouple technique)测得的不同冷却制度下的开始结晶温度以及不同温度下的孕育时间就可以判断出渣膜不同位置处是否有晶体析出.
![]()
图 4 浸入式水冷铜探头法示意图Figure 4. Schematic of the experimental apparatus for copper-finger dig test双丝法和水冷铜探头法的测试过程中，渣膜的位置是固定的，然而实际连铸过程中结晶器上下往复振动，固态渣膜与结晶器之间可能还存在相对运动，可见现有用于模拟渣膜形成的实验方法还不能对固态渣膜的运动情况进行模拟，结晶器内不同位置处固态渣膜微观结构的变化还有待进一步研究.
2. 结晶器内渣膜传热的研究现状
坯壳与结晶器之间的水平传热主要有传导和辐射两种传热方式[14]. 由于铸坯表面与结晶壁之间填充着固渣膜、液渣膜和气隙三层介质，传导传热又可以分为渣膜的导热以及气隙层的导热. 气隙层的导热主要通过界面热阻，即气隙层的厚度与空气导热系数的比值来表征. 由于铸坯表面温度较高，通过渣膜的热量中有一部分来自于辐射传热，这部分能量在传播过程中会被介质反射、散射或者吸收. 在研究辐射传热时，可以根据电磁学的相关理论对辐射传热进行数值计算，也可以通过测试渣膜的光学性质(反射率、透过率和吸收率)来表征辐射传热的强弱. 下面将从界面热阻、渣膜导热系数、辐射传热的计算方法以及光学性质的影响因素四个方面总结前人在保护渣传热方面所做的研究工作.
2.1 保护渣固态渣膜界面热阻
保护渣固态渣膜与结晶器的界面如图 6所示. 保护渣固态渣膜的界面热阻指的是固态渣膜与结晶器壁之间气隙层的导热热阻.
![]()
图 6 保护渣固态渣膜与结晶器的界面示意图Figure 6. Interface diagram between the solid slag film and mold根据傅里叶导热定律，界面热阻可以表示为：
$$ R_{\mathrm{int}}=\frac{T_{\mathrm{s}}-T_{\mathrm{cu}}}{q_{\mathrm{con}}}=\frac{d_{\mathrm{air}}}{k_{\mathrm{air}}} $$ (3) 式中，Rint是界面热阻，m2·K·W-1；Ts是固态渣膜与气隙界面的温度，K；Tcu是结晶器壁表面的温度，K；dair是气隙层的厚度，m；kair是空气的导热系数，W·m-1·K-1. 液渣完全凝固过后，固渣膜表面的具体位置很难确定，所以式(3)中Ts和dair是两个难以测量准确的参数. 现有文献中关于界面热阻的研究都是围绕着如何准确得到Ts和dair的值而进行的. 可以基于稳态条件下渣膜内部以及冷却介质的温度分布计算Ts，也可以设法获得dair的值，再根据空气的导热系数计算出界面热阻.
基于温度分布计算界面热阻可以通过平板法来研究. Cho利用一个可以上下移动的水冷铜探头对置于一块平板上的液态保护渣进行冷却[15]，通过测量铜探头内部的温度分布并结合数值计算得到了保护渣的界面热阻，实验设备如图 7所示. 实验过程中，渣膜厚度可以通过改变铜探头的位置进行控制. 研究结果表明保护渣的界面热阻在0.0005~0.002 m2·K·W-1范围内，而且随着固态渣膜结晶层厚度的增加而增加. Cho的研究结果虽然给出了结晶层厚度与界面热阻之间的数值关系，但是没有具体分析保护渣与平板之间气隙的形成过程以及固态渣膜微观组织对界面热阻的影响.
![]()
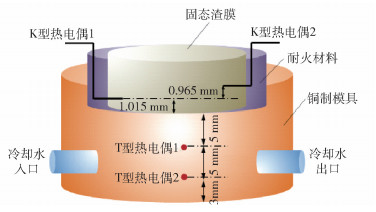
Park与Sohn也是基于温度分布来计算界面热阻[16]，不同的地方在于Park等是将高温下的保护渣直接倒入位置固定的铜制水冷模具中使保护渣凝固，并且对固态渣膜的微观组织与界面热阻的关系进行了研究，实验设备如图 8所示. 结果表明保护渣的界面热阻在0.0004~0.0008 m2·K·W-1范围内，而且随渣膜平均波纹度的增加而增加. Park等认为界面热阻的大小取决于渣膜收缩的程度，固态渣膜中的玻璃在回热再结晶的过程中晶粒更容易长大，导致渣膜的收缩程度比液相向晶体转变过程的收缩程度要大，所以即使固态渣膜结晶比较低，界面热阻可能由于渣膜再结晶过程的收缩而变大.
![]()
如果利用渣膜及冷却介质的温度分布计算界面热阻，通常要将实验测试与数值计算结合起来，但是也有一些研究者通过测量固态渣膜的表面粗糙度来表征气隙层的厚度，从而得到界面热阻的大小[17-18]. Tsutsumi等利用激光共聚焦显微镜观察了不同冷却速度下渣膜的表面，采用轮廓波峰与波谷之差当作表面粗糙度，并且将表面粗糙度的二分之一认为是气隙层的厚度[17]. 结果表明保护渣界面热阻在0.0002~0.0006 m2·K·W-1之间，凝固后固渣的表面粗糙度主要取决于冷却速度的大小，液渣冷却速度越大，固渣表面越光滑，界面热阻越小. 当冷却速度一定时，固渣的表面粗糙度随保护渣临界冷却速度的增加而增加，但这并不意味着渣膜的表面粗糙度会随结晶度的增加而增加. Long等通过对浸入式水冷铜探头获取到的固态渣膜研究后发现[19]，固态渣膜的表面粗糙度在整个渣膜的生长过程中变化不大，这也就意味着表面粗糙度与渣膜是否结晶没有关系.
综合上述学者的研究结果，基本可以确定渣膜的界面热阻在0.0002~0.002 m2·K·W-1之间，而且结晶(包括玻璃的回热再结晶)对增加固态渣膜的界面热阻有一定的作用，但促进保护渣结晶却并不一定能增加固态渣膜的表面粗糙度. 此外，上述界面热阻的测试结果是在固态渣膜完全形成以后得到的，这意味着现有文献的研究结果只能反映结晶器中下部固态渣膜的界面热阻. 但是在结晶器的弯月面处，固态渣膜较薄，辐射传热所占的比例高[20]，界面热阻的大小及传热机理可能与结晶器中下部不同. 由于控制弯月面处的传热是改善铸坯表面质量的关键，今后有必要针对弯月面处的界面热阻及传热机理进行深入研究.
2.2 保护渣导热系数
关于固态渣膜传导传热的研究主要是针对渣膜导热系数的研究. 根据德拜公式，绝缘固体材料的导热系数kcon可以表示为[21]：
$$ k_{\mathrm{con}}=\frac{1}{3} C_{\mathrm{v}} v l_{\mathrm{p}} $$ (4) 式中：Cv是物体的体积比热容，J·m-3·K-1；v是声速，m·s-1；lp是声子平均自由程，m. 声子平均自由程与温度有关. 低温下，声子平均自由程随温度的增加而增加，当温度超过德拜温度以后，比热容和声速接近常数，而声子平均自由程由于声子密度的增加而逐渐降低[21]. 有观点认为导热系数除了与温度有关外，还与高温下的熔渣结构有关，熔渣聚合度越低，熔渣中随机分布的网络结构越多，这些结构的存在会限制声子平均自由程的增加从而导致热扩散系数下降[22]. 现有文献中关于保护渣导热系数的测试方法主要有瞬时热线法和激光脉冲法两种，瞬时热线法是将一根很细的金属加热丝(热线)置于保护渣的中心，热线升温速度的快慢与保护渣的导热系数有如下关系[22-24]：
$$ k_{\mathrm{con}}=\frac{q}{4 {\rm{ \mathsf{ π}}}} \frac{\partial \ln t}{\partial \Delta T} $$ (5) 式中：q是单位长度热线的加热功率，W·m-1；t是通电时间，s；ΔT是通电时间内热线温度的变化，K. 将lnt随ΔT的关系用直线拟合得到直线的斜率，再根据式(5)就能计算出保护渣的导热系数. 由于液渣具有一定的导电性，热线漏电可能会给测量结果带来一定误差. 另一种测量保护渣导热系数的方法是激光脉冲法. 测试过程中须要给样品的表面提供一个瞬时的激光脉冲，当激光照射到样品表面时，样品表面温度升高，同时开始向样品内部传热. 通过检测样品背面温度随时间的变化，就能计算出样品的热扩散系数. 样品热扩散系数与样品背面温度达到最高温度的二分之一所需的时间有如下关系[25]：
$$ k_{\mathrm{p}}=\frac{0.1388 d^{2}}{t_{1 / 2}} $$ (6) 式中：kp是热扩散系数，m2·s-1；d是样品厚度，m；t1/2是样品背面温度达到最高温度的二分之一所需的时间，s. 在得到热扩散系数后，热扩散系数与导热系数具有如下关系：
$$ k_{\mathrm{con}}=k_{\mathrm{p}} C_{\mathrm{p}} \rho $$ (7) 式中：Cp是样品比热容，J·kg-1·K-1；ρ是样品密度，kg·m-3. 激光脉冲法测试过程中，如果施加给样品表面的辐射能被样品内部吸收，那么样品背面温度的升高就不完全是导热引起的，这将会给测试结果带来误差，特别是在样品表面积较大的时候，这种误差可能会更大. 激光脉冲法是对导热系数的间接测试，而瞬时热线法可以直接测得导热系数的大小. Andersson利用瞬时热线法研究了室温至1000 ℃范围内保护渣的导热系数[22]，结果发现当温度低于770 ℃时，保护渣的导热系数随温度的升高而逐渐增加；当温度超过770 ℃时，保护渣的导热系数随温度的升高而急剧下降. 在770 ℃时，保护渣的导热系数大概为1.65 W·m-1·K-1，而且保护渣的结晶度越高，保护渣的导热系数越大.
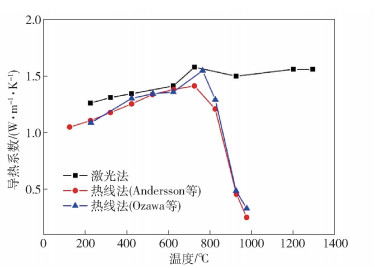
几乎所有瞬时热线法的测试结果都表明随着温度的升高，保护渣的导热系数呈现出先增加后减小的趋势. 但是激光脉冲法的测试结果却有所不同. Waseda等激光脉冲法的测试结果表明[26]，在1100~1300 ℃范围内，保护渣的热扩散系数在4×10-7~6×10-7 m2·s-1的范围内，假设保护渣比热容为1000 J·K-1·kg-1，密度为2500 kg·m-3，那么导热系数在1.0~1.5 W·m-1·K-1范围内. 可见激光脉冲法测得的导热系数不会呈现出随着温度的升高而急剧减小的趋势. 不同研究者利用两种方法得到的导热系数随温度变化的关系如图 9所示[20].
![]()
从图 9中可以看出，在800 ℃以下，瞬时热线法与激光脉冲法得到的导热系数的值是接近的，且都呈现出随温度的升高而增加的趋势. 但是在800 ℃以上，热线法测得的导热系数随着温度的升高急剧减小至0.5 W·m-1·K-1以下，而激光脉冲法测得的导热系数稳定在1.5 W·m-1·K-1左右.
2.3 保护渣辐射传热的测试及计算方法
连铸过程中被冷却水带走的热量包括两个部分，一部分是通过渣膜的传导传热，另外一部分是来自高温坯壳表面的辐射传热. 目前关于保护渣辐射传热的研究主要以固态渣膜的辐射热通量为主. Wang与Cramb利用一个红外发射器对置于水冷铜柱上的固态的渣膜样品进行加热[27]，通过测量铜柱不同位置处的温度可以得到通过固态渣膜的热流密度，实验结果表明结晶渣膜的透过率比玻璃渣膜的透过率低. 关于保护渣辐射传热的研究，更多的是采用数值计算的方法对辐射热流或渣膜的光学性质进行定量计算. 下面针对现有文献中报道的关于保护渣辐射传热的计算方法及结果进行简要的介绍.
光线在空间的传播过程可以结合电磁学理论进行解释，通过介质的辐射热流与介质温度之间的关系无法像导热热流那样用简单的表达式描述出来. 在计算时往往要做很多简化及近似处理. 如果介质的光学厚度(介质厚度与消光系数的乘积)较大且介质内部温度梯度较小，可以用罗斯兰扩散方程(rosseland diffusion equation)计算辐射传热系数[28]：
$$ k_{\mathrm{rad}}=\frac{16 n^{2} \sigma T^{3}}{3 \alpha_{\mathrm{p}}} $$ (8) 式中：krad是辐射传热系数，W·m-1·K-1；n是折射指数；σ是玻尔兹曼常数，W·m-2·K-4；T是介质的温度，K；αp是平均吸收系数，m-1. 通过介质的辐射热流密度可以表示为：
$$ q_{\mathrm{rad}}=k_{\mathrm{rad}} \frac{T_{1}-T_{2}}{d} $$ (9) 式中：qrad是通过某层介质的辐射热流密度，W·m-2；T1和T2分别是介质两个表面的温度，K；d是介质的厚度，m. 连铸过程中结晶器内渣膜的温度梯度较大，而且光学厚度较小，不能满足罗斯兰扩散方程的使用条件，利用式(9)计算得到的渣膜的辐射热流占总热流的99.4%[28]，这显然与实际情况不符，因此式(8)不能用于计算渣膜的辐射传热.
如果将渣膜看作是灰体(单色吸收率与波长无关)且渣膜厚度均匀，那么通过渣膜的辐射传热可以简化为两块平行的无限大平板之间的辐射换热问题，此时辐射热流密度可以表示为[28]：
$$ q_{\mathrm{rad}}=\beta\left(T_{1}^{4}-T_{2}^{4}\right) $$ (10) 式中：T1和T2分别是两块平板的温度，K；β可以表示为：
$$ \beta=\frac{n^{2} \sigma}{0.75 \alpha d+\frac{1}{\varepsilon_{1}}+\frac{1}{\varepsilon_{2}}-1} $$ (11) 式中，ε1和ε2分别是两块平板的黑度. α是介质的吸收系数，m-1.
根据式(10)得到的通过液态渣膜辐射热流占总热流的32%~47%，而通过结晶的固态渣膜的辐射热流仅占总热流的3%~10%.
连铸过程中，坯壳表面以及结晶器表面会对光线进行反射. 针对这一特点，Diao等提出用辐射热交换模型计算坯壳与结晶器之间的辐射热通量[29-30]. 这个模型的基本假设条件有三个：1)将坯壳与结晶器之间的固渣膜、液渣膜以及气隙层看作是一种介质；2)将坯壳向外辐射能与结晶器向外辐射能之差看作是坯壳的有效辐射，这部分能量与渣膜透过率的乘积等于结晶器净得到的能量；3)坯壳净失去的能量等于结晶器净得到的能量.
坯壳或结晶器向外辐射的能量包括两个部分，一是自身向外的辐射能，二是被自身反射回去的辐射能. 再根据第二个假设条件和第三个假设条件，可以得到下面的方程组：
$$ \left\{\begin{array}{l} J_{1}=E_{1}+\left(1-\alpha_{1}\right) G_{1} \\ J_{2}=E_{2}+\left(1-\alpha_{2}\right) G_{2} \\ J_{1}-G_{1}=G_{2}-J_{2}=q_{\lambda} \\ T_{\mathrm{a}}=\frac{q_{\lambda}}{J_{1}-J_{2}} \end{array}\right. $$ (12) 式中：J1和J2分别是坯壳和结晶器向外的单色辐射能，W·m-3；E1和E2分别是坯壳和结晶器自身向外的单色辐射能，W·m-3；数值上等于黑度与黑体单色辐射能的乘积. G1和G2分别是到达坯壳表面和结晶器表面的单色辐射能，W·m-3；α1和α2分别是坯壳和结晶器的吸收率，根据基尔霍夫定律，吸收率近似等于黑度. qλ是坯壳净失去的单色辐射热流，W·m-3，数值上等于结晶器净得到的能量，Ta是渣膜透过率. 根据式(12)可得通过渣膜的单色辐射热流密度的表达式为：
$$ q_{\lambda}=\frac{E_{\mathrm{b1}, \lambda}-E_{\mathrm{b} 2, \lambda}}{\frac{1}{\varepsilon_{1}}+\frac{1}{\varepsilon_{2}}+T-2} $$ (13) 式中，ε1和ε2分别是坯壳和结晶器表面的黑度. Eb1, λ和Eb2, λ表示黑体单色辐射能，W·m-3；可以根据普朗克定律计算：
$$ E_{\mathrm{b}, \lambda}=\frac{c_{1} \lambda^{-5}}{\mathrm{e}^{\frac{c_{2}}{\lambda T}}-1} $$ (14) 式中：c1是普朗克第一常数，其值为3.742×10-16 W·m2，c2是普朗克第二常数，其值为0.0144 m·K；λ是波长，m；T是介质温度，K. 单色辐射热流对波长积分就可以得到通过渣膜的辐射热流密度. Diao等利用傅里叶红外光谱(FTIR)测得了固态渣膜的透过率并利用上述计算方法研究了过渡族金属氧化物对保护渣辐射传热的影响，结果发现过渡族金属氧化物(MnO、FeO和TiO2)的加入能有效的降低通过渣膜的辐射传热[29-31].
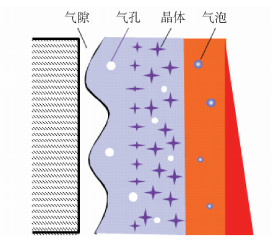
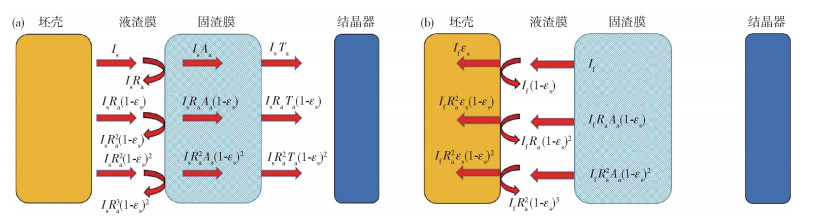
实际上光线不仅在气隙层内进行反射，在固态渣膜内部以及液态渣膜内部都要进行来回多次的反射. Susa等考虑了光线在液渣膜内部的多次反射提出用光线路径追踪法计算通过渣膜的辐射热通量[32]. 路径追踪法的基本假设条件有以下几个：(1)坯壳与结晶器之间只有固渣膜和液渣膜两种介质，且液渣对辐射的吸收忽略不计；(2)不考虑固态渣膜内部的多重反射；(3)固态渣膜净得到的辐射能可以传递到结晶器表面. 光线在液渣内部的传播路径如图 10所示.
![]()
图 10 光线在坯壳与固态渣膜之间的多重反射. (a) 能量由坯壳表面发射；(b) 能量由固液界面发射Figure 10. Multiple reflections between the shell and solid slag film: (a) emission from the shell; (b) emission from the interface从图 10中可以看出固态渣膜获得的能量包括两部分，一部分是坯壳表面发出，被固态渣膜吸收的能量IA by flux；另一部分是坯壳表面发出，透过固态渣膜的能量IT. 与此同时，固态渣膜也在向外辐射能量，其中被坯壳表面吸收的能量IA by steel是固态渣膜损失的能量. 根据能量守恒，固态渣膜净得到的能量可以表示为：
$$ I_{\lambda}=I_{\mathrm{A} \text { by flux }}+I_{\mathrm{T}}-I_{\mathrm{A} \text { by steel }} $$ (15) 式中：Iλ表示固态渣膜净得到的单色辐射能，W·m-3；IA by flux表示被固态渣膜吸收的单色辐射能，W·m-3；IT表示透过固态渣膜的单色辐射能，W·m-3；IA by steel 表示从渣膜固液界面发射后被坯壳吸收的单色辐射能，W·m-3. 分别对每一次反射过程中的这三种辐射能进行累加求和可以得到IA by flux，IT以及IA by steel的表达式：
$$ \begin{gathered} I_{\mathrm{A} \text { by flux }}=I_{\mathrm{s}} A_{\mathrm{a}}+\left(1-\varepsilon_{\mathrm{s}}\right) R_{\mathrm{a}} A_{\mathrm{a}} I_{\mathrm{s}}+\cdots= \\ I_{\mathrm{s}} A_{\mathrm{a}}\left(1-\left(1-\varepsilon_{\mathrm{s}}\right) R_{\mathrm{a}}\right)^{-1} \end{gathered} $$ (16) $$ \begin{gathered} I_{\mathrm{T}}=I_{\mathrm{s}} T_{\mathrm{a}}+\left(1-\varepsilon_{\mathrm{s}}\right) R_{\mathrm{a}} T_{\mathrm{a}} I_{\mathrm{s}}+\cdots= \\ I_{\mathrm{s}} T_{\mathrm{a}}\left(1-\left(1-\varepsilon_{\mathrm{s}}\right) R_{\mathrm{a}}\right)^{-1} \end{gathered} $$ (17) $$ \begin{gathered} I_{\mathrm{A} \text { by steel }}=I_{\mathrm{f}} \varepsilon_{\mathrm{s}}+\left(1-\varepsilon_{\mathrm{s}}\right) R_{\mathrm{a}} \varepsilon_{\mathrm{s}} I_{\mathrm{f}}+\cdots= \\ I_{\mathrm{f}} \varepsilon_{\mathrm{s}}\left(1-\left(1-\varepsilon_{\mathrm{s}}\right) R_{\mathrm{a}}\right)^{-1} \end{gathered} $$ (18) 式(16)~式(18)中Ra，Aa和Ta分别表示固态渣膜的表观反射率、表观吸收率和表观透过率. εs表示坯壳表面的黑度，Is和If分别表示坯壳表面和渣膜固液界面向外的单色辐射能，W·m-3，根据式(14)可以得到Is和If的表达式：
$$ I_{\mathrm{s}}=n^{2} \varepsilon_{\mathrm{s}} c_{1} \lambda^{-5}\left(\exp \left(\frac{c_{2}}{\lambda T_{\mathrm{s}}}\right)-1\right)^{-1} $$ (19) $$ I_{\mathrm{f}}=n^{2} A_{\mathrm{a}} c_{1} \lambda^{-5}\left(\exp \left(\frac{c_{2}}{\lambda T_{\mathrm{f}}}\right)-1\right)^{-1} $$ (20) 式(19)和式(20)中Ts和Tf分别表示坯壳表面和渣膜固液界面的温度，K. 将式(16)~(18)代入式(15)可以得到Iλ的表达式：
$$ \begin{gathered} I_{\lambda}=\frac{n^{2} c_{1}}{\lambda^{5}\left(1-\left(1-\varepsilon_{\mathrm{s}}\right) R_{\mathrm{a}}\right)}\left(\frac{\left(1-R_{\mathrm{a}}\right) \varepsilon_{\mathrm{s}}}{\exp \left(c_{2} / \lambda T_{\mathrm{s}}\right)-1}-\right. \\ \left.\frac{A_{\mathrm{a}} \varepsilon_{\mathrm{s}}}{\exp \left(c_{2} / \lambda T_{\mathrm{f}}\right)-1}\right) \end{gathered} $$ (21) 式(21)对波长积分就可以得到通过固态渣膜的辐射热通量. Susa等利用路径追踪法研究了结晶和铁氧化物对保护渣辐射传热的影响[32-33]，结果发现通过渣膜的辐射传热主要取决于反射率. 晶体可以增加渣膜的反射率并且降低透过率，因此能有效的降低通过渣膜的辐射热流密度. 但铁氧化物的加入却不能降低辐射传热，这是由于含有铁氧化物的渣膜的反射率比不含铁氧化物时的反射率要小.
从以上几位学者的研究结果中不难发现，人们对结晶如何影响渣膜的辐射传热所持的观点基本一致，一方面，渣膜中的晶体可以增加消光系数，使渣膜的透过率下降；另一方面晶体能增加固态渣膜的反射率. 这两方面的因素导致晶体能有效的控制通过渣膜的辐射传热. 但是关于过渡族金属氧化物是否能够降低辐射传热，不同的研究者基于不同的计算模型得到了不同的结论. 以上关于辐射传热的计算模型都只是考虑了单纯的辐射传热，而高温下坯壳向结晶器的传热是导热和辐射的耦合传热，实验室的测试过程也很难避免导热的参与. 要想准确计算通过渣膜的辐射传热，必须建立传导与辐射的耦合传热模型，尤其是针对相变温度不固定的熔渣的耦合传热过程.
2.4 保护渣固态渣膜的光学性质
在固态渣膜温度分布一定的情况下，通过渣膜的辐射热流主要取决于渣膜的光学性质，渣膜中的粒子对光学性质的影响可以根据粒子的尺寸分为以下几类.
(1) 分子大小范围内的Fe2+、Fe3+、Mn2+、Ti4+等金属阳离子会对某些波长范围内的电磁波进行选择性的吸收. TiO2在渣中可以改变分子结构的对称性，造成分子偶极距变化，同时分子振动加强，红外吸收率也随之增加，而Fe2+和Fe3+可以增加1000 nm附近红外光的吸收系数[31].
(2) 直径在1~100 nm范围内的胶体粒子对辐射传热的影响遵循瑞利散射定律[34].
(3) 直径在0.05~10 μm的微小晶体以及铁氧化物被碳还原后形成的金属铁颗粒对辐射传热的影响遵循米氏散射定律. Yoon等的研究发现保护渣熔化过程中[35]，加入的Fe2O3能够在石墨坩埚内被CO还原为直径小于5 μm的金属铁颗粒，这种弥散分布的金属铁颗粒可以增加玻璃渣膜的消光系数.
(4) 直径大于10 μm的晶体以及碳酸盐或硫酸盐分解后形成的气泡对光学性质的影响可用几何光学，即斯涅耳定律及菲涅尔公式研究[36]. Susa的研究发现对于不含铁氧化物的保护渣，固态渣膜对波长大于1200 nm的红外光的反射率随着晶体粒度的增加而增加，而透过率随晶体粒度的增加而减小，但是对于含有铁氧化物的保护渣，晶体粒度对光学性质的影响不大. 除了晶体外，固态渣膜中的气孔同样对光学性质有影响，Rousseau等发现多孔材料的光学性质不仅与孔隙度有关[37]，还与气孔尺寸有关. 在孔隙度一定的情况下，气孔的索特平均直径越小，多孔介质对中红外光(波长在3~50 μm范围内)的反射率越大，这意味着固态渣膜中尺寸分布均匀的小孔可能会对控制辐射传热起到一定的作用.
3. 渣膜形成及传热研究的展望
(1) 利用双丝法和水冷铜探头法已经可以模拟出渣膜的形成过程，但是关于实际结晶器内固态渣膜的形成过程和运动情况的研究还不完善. 连铸过程中结晶器内不同位置处固态渣膜表面微观结构的变化还值得进一步研究.
(2) 关于渣膜导热系数及界面热阻，国内外学者已经做了大量的研究，但不同的测试条件及实验方法得到的结果并不完全一致. 无论是导热系数还是界面热阻，测试原理都与傅里叶导热定律有关，但这两个量的测定都涉及到高温介质，因此在实验以及计算中须要设法排除辐射传热的影响.
(3) 现有关于渣膜辐射传热的计算方法没有考虑三层介质内部的多重反射，并且忽略了渣膜传热是传导与辐射的耦合这一条件. 如果要准确计算通过渣膜的辐射热流，须要建立传导与辐射的耦合传热模型，以便描述渣膜形成过程中导热热流及辐射热流随时间的变化规律.
(4) 目前关于渣膜光学性质的测试都是在常温下进行的. 高温下液渣光学性质的研究，尤其是液渣中微小粒子及气泡对光学性质的影响还不完善，结晶器弯月面处渣膜的传热机理还不清楚. 这方面内容一方面可以通过对设备的改进实现高温光学性质的测试，另一方面可以借助相关的光学理论进行定量描述.
-
![]()
图 2 热丝法实验装置示意图. (a) 工业摄像机；(b) 样品室；(c) 单热电偶；(d) 双热电偶；(e) 加热装置；(f) 计算机
Figure 2. Schematic diagram of experimental apparatus for hot thermocouple technique: (a) industrial camera; (b) sample chamber; (c) single hot thermocouple; (d) double hot thermocouple; (e) hot thermocouple driver; (f) computer
![]()
图 3 双丝法模拟的渣膜形成过程, 其中通道1和2分别为模拟结晶器侧固渣温度和坯壳侧液渣温度条件. (a) 10 s；(b) 50 s；(c) 300 s；(d) 301 s[10]
Figure 3. Formation process of slag film simulated by DHTT, where Channel 1 and 2 simulate the temperature condition of solidified slag film near the mold wall and liquid slag near the shell, respectively: (a) 10 s; (b) 50 s; (c) 300 s; (d) 301 s[10]
![]()
图 4 浸入式水冷铜探头法示意图
Figure 4. Schematic of the experimental apparatus for copper-finger dig test
![]()
图 6 保护渣固态渣膜与结晶器的界面示意图
Figure 6. Interface diagram between the solid slag film and mold
![]()
![]()
![]()
-
[1] Mills K C, Fox A B, Li Z, et al. Performance and properties of mould fluxes. Ironmak Steelmak, 2005, 32(1): 26 doi: 10.1179/174328105X15788
[2] Mills K C, Fox A B. The role of mould fluxes in continuous casting-So simple yet so complex. ISIJ Int, 2003, 43(10): 1479 doi: 10.2355/isijinternational.43.1479
[3] Mills K C, Courtney L, Fox A B, et al. The use of thermal analysis in the determination of the crystalline fraction of slag films. Thermochim Acta, 2002, 391(1-2): 175 doi: 10.1016/S0040-6031(02)00175-2
[4] 张平, 魏庆成, 王家荫, 等. 连铸结晶器中保护渣渣膜传热的研究现状. 钢铁研究学报, 1995, 7(4): 74 https://www.cnki.com.cn/Article/CJFDTOTAL-IRON504.014.htm Zhang P, Wei Q C, Wang J Y, et al. Present state of research on heat transfer of casting flux film in continuous casting mold. J Iron Steel Res, 1995, 7(4): 74 https://www.cnki.com.cn/Article/CJFDTOTAL-IRON504.014.htm
[5] Meng Y, Thomas B G. Simulation of microstructure and behavior of interfacial mold slag layers in continuous casting of steel. ISIJ Int, 2006, 46(5): 660 doi: 10.2355/isijinternational.46.660
[6] Kashiwaya Y, Cicutti C E, Cramb A W, et al. Development of double and single hot thermocouple technique for in situ observation and measurement of mold slag crystallization. ISIJ Int, 1998, 38(4): 348 doi: 10.2355/isijinternational.38.348
[7] Zhou L J, Wang W L, Liu R, et al. Computational modeling of temperature, flow, and crystallization of mold slag during double hot thermocouple technique experiments. Metall Mater Trans B, 2013, 44(5): 1264 doi: 10.1007/s11663-013-9864-2
[8] Li J, Wang W L, Wei J, et al. A kinetic study of the effect of Na2O on the crystallization behavior of mold fluxes for casting medium carbon steel. ISIJ Int, 2012, 52(12): 2220 doi: 10.2355/isijinternational.52.2220
[9] Lu B X, Chen K, Wang W L, et al. Effects of Li2O and Na2O on the crystallization behavior of lime-aliminum-based mold flux for casting high-Al steels. Metall Mater Trans B, 2014, 45(4): 1496 doi: 10.1007/s11663-014-0063-6
[10] Gao J X, Wen G H, Sun Q H, et al. The influence of Na2O on the solidification and crystallization behavior of CaO-SiO2-Al2O3 based mold flux. Metall Mater Trans B, 2015, 46(4): 1850 doi: 10.1007/s11663-015-0366-2
[11] Wen G H, Tang P, Yang B, et al. Simulation and characterization on heat transfer through mould slag film. ISIJ Int, 2012, 52(7): 1179 doi: 10.2355/isijinternational.52.1179
[12] Wen G H, Zhu X B, Tang P, et al. Influence of raw material type on heat transfer and structure of mould slag. ISIJ Int, 2011, 51(7): 1028 doi: 10.2355/isijinternational.51.1028
[13] Yang C L, Wen G H, Sun Q H, et al. Evolution of temperature and solid slag film during solidification of mold fluxes. Metall Mater Trans B, 2017, 48(2): 1292 doi: 10.1007/s11663-017-0917-9
[14] Mills K C. A short history of mould powders. Ironmak Steelmak, 2017, 44(5): 326 doi: 10.1080/03019233.2017.1288367
[15] Cho J, Shibata H, Emi T, et al. Thermal resistance at the interface between mold flux film and mold for continuous casting of steels. ISIJ Int, 1998, 38(5): 440 doi: 10.2355/isijinternational.38.440
[16] Park J Y, Sohn Ⅱ. Evaluating the heat transfer phenomenon and the interfacial thermal resistance of mold flux using a copper disc mold simulator. Int J Heat Mass Transfer, 2017, 109: 1014 doi: 10.1016/j.ijheatmasstransfer.2017.02.092
[17] Tsutsumi K, Nagasaka T, Hino M. Surface roughness of solidified mold flux in continuous casting process. ISIJ Int, 1999, 39(11): 1150 doi: 10.2355/isijinternational.39.1150
[18] Shibata H, Kondo K, Suzuki M, et al. Thermal resistance between solidifying steel shell and continuous casting mold with intervening flux film. ISIJ Int, 1996, 36(Suppl): S179 doi: 10.2355/isijinternational.36.Suppl_S179
[19] Long X, He S P, Wang Q, et al. Structure of solidified films of mold flux for peritectic steel. Metall Mater Trans B, 2017, 48(3): 1652 doi: 10.1007/s11663-017-0965-1
[20] Mill K C. Structure and properties of slags used in the continuous casting of steel: Part 1 conventional mould powders. ISIJ Int, 2016, 56(1): 1 doi: 10.2355/isijinternational.ISIJINT-2015-231
[21] Lee D W, Kingery W D. Radiation energy transfer and thermal conductivity of ceramic oxides. J Am Ceram Soc, 1960, 43(11): 594 doi: 10.1111/j.1151-2916.1960.tb13623.x
[22] Anderson S P, Eggertson C. Thermal conductivity of powders used in continuous casting of steel. Ironmak Steelmak, 2015, 42(6): 456 doi: 10.1179/1743281214Y.0000000250
[23] Susa M, Watanabe M, Ozawa S, et al. Thermal conductivity of CaO-SiO2-Al2O3 glassy slags: its dependence on molar ratios of Al2O3/CaO and SiO2/Al2O3. Ironmak Steelmak, 2007, 34(2): 124 doi: 10.1179/174328107X165672
[24] Ozawa S, Susa M. Effect of Na2O additions on thermal conductivities of CaO-SiO2 slags. Ironmak Steelmak, 2005, 32(6): 487 doi: 10.1179/174328105X48179
[25] Hayashi M, Abas R A, Seetharaman S. Effect of crystallinity on thermal diffusivities of mould fluxes for the continuous casting of steels. ISIJ Int, 2004, 44(4): 691 doi: 10.2355/isijinternational.44.691
[26] Waseda Y, Masuda M, Watanabe K, et al. Thermal diffusivitites of continuous casting powders for steel at high temperature. High Temp Mater Processes, 1994, 13(4): 267 doi: 10.1515/HTMP.1994.13.4.267
[27] Wang W L, Cramb A W. The observation of mold flux crystallization on radiative heat transfer. ISIJ Int, 2005, 45(12): 1864 doi: 10.2355/isijinternational.45.1864
[28] Cho J, Shibata H, Emi T, et al. Radiative heat transfer through mold flux film during initial solidification in continuous casting of steel. ISIJ Int, 1998, 38(3): 268 doi: 10.2355/isijinternational.38.268
[29] Diao J, Xie B, Wang N H, et al. Effect of transition metal oxides on radiative heat transfer through mold flux film in continuous casting of steel. ISIJ Int, 2007, 47(9): 1294 doi: 10.2355/isijinternational.47.1294
[30] Diao J, Xie B, Xiao J P, et al. Radiative heat transfer in transition metal oxides contained in mold fluxes. ISIJ Int, 2009, 49(11): 1710 doi: 10.2355/isijinternational.49.1710
[31] 刁江, 谢兵. 基于FTIR和XRD的降低连铸保护渣红外辐射传热研究. 光谱学与光谱分析, 2009, 29(2): 336 doi: 10.3964/j.issn.1000-0593(2009)02-0336-04 Diao J, Xie B. Research on reducing mold flux's radiative heat transfer based on FTIR and XRD. Spectrosc Spect Anal, 2009, 29(2): 336 doi: 10.3964/j.issn.1000-0593(2009)02-0336-04
[32] Susa M, Kushimoto A, Toyota H, et al. Effects of both crystallization and iron oxides on the radiative heat transfer in mould fluxes. ISIJ Int, 2009, 49(11): 1722 doi: 10.2355/isijinternational.49.1722
[33] Susa M, Kushimoto A, Endo R, et al. Controllability of radiative heat flux across mould flux films by cuspidine grain size. ISIJ Int, 2011, 51(10): 1587 doi: 10.2355/isijinternational.51.1587
[34] Bucholtz A. Rayleigh-scattering calculations for the terrestrial atmosphere. Appl Opt, 1995, 34(15): 2765 doi: 10.1364/AO.34.002765
[35] Yoon D W, Cho J W, Kim S H. Scattering effect of iron metallic particles on the extinction coefficient of CaO-SiO2-B2O3-Na2O-Fe2O3-CaF2 glasses. Metall Mater Trans B, 2016, 47(5): 2785 doi: 10.1007/s11663-016-0765-z
[36] Yang C L, Wen G H, Zhu X F, et al. In situ observation and numerical simulation of bubble behavior in CaO-SiO2 based slag during isothermal and nonisothermal processes. J Non-Cryst Solids, 2017, 464: 56 doi: 10.1016/j.jnoncrysol.2017.03.028
[37] Rousseau B, Meneses D D S, Echegut P, et al. Textural parameters influencing the radiative properties of a semitransparent porous media. Int J Therm Sci, 2011, 50(2): 178 doi: 10.1016/j.ijthermalsci.2010.10.001
-
期刊类型引用(6)
1. 陈玉凤，刘宇航，宋景凌，李恒华，周旋，杨树峰，刘威，李京社. 25CrMnMo钢表面缺陷成因分析及控制. 河北冶金. 2024(03): 45-50 . 
百度学术
2. 高宇波，管蒙寒，张建斌，包燕平. 高拉速生产小方坯包晶钢表面质量控制与改善. 炼钢. 2022(02): 49-53 . 百度学术
3. 文光华，陈富杭，蒋文波，侯自兵，唐萍. 连铸结晶器“自适应保护渣”理论及应用. 工程科学学报. 2022(09): 1558-1565 . 本站查看
4. 何宇明，何生平. 结晶器保护渣的润滑与传热控制功能剖析. 连铸. 2021(02): 2-6 . 百度学术
5. 张磊，翟冰钰，王万林. 保护渣晶粒尺寸对传热性能的影响. 江西冶金. 2021(02): 20-25 . 百度学术
6. 李超，任素波，胡正才，游佳泉. 连铸结晶器内坯壳安全凝固的研究. 重型机械. 2020(01): 33-38 . 百度学术
其他类型引用(2)
下载:
计量
- 文章访问数: 1583
- HTML全文浏览量: 716
- PDF下载量: 102
- 被引次数: 8
